標簽:方式 變換 變量 不必要 系統 變異 alt 旋轉門 max
1 遗传算法概述
遗传算法(Genetic Algorithm,GA)是进化计算的一部分,是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法简单、通用,鲁棒性强,适于并行处理。
2 遗传算法的特点和应用
遗传算法是一类可用于复杂系統优化的具有鲁棒性的搜索算法,与传统的优化算法相比,具有以下特点:
(1)以决策變量的编码作为运算对象。传统的优化算法往往直接利用决策變量的实际值本身来进行优化计算,但遗传算法是使用决策變量的某种形式的编码作为运算对象。这种对决策變量的编码处理方式,使得我们在优化计算中可借鉴生物学中染色体和基因等概念,可以模仿自然界中生物的遗传和进化激励,也可以很方便地应用遗传操作算子。
(2)直接以适应度作为搜索信息。传统的优化算法不仅需要利用目标函数值,而且搜索过程往往受目标函数的连续性约束,有可能还需要满足“目标函数的导数必须存在”的要求以确定搜索方向。遗传算法仅使用由目标函数值變換来的适应度函数值就可确定进一步的搜索范围,无需目标函数的导数值等其他辅助信息。直接利用目标函数值或个体适应度值也可以将搜索范围集中到适应度较高部分的搜索空间中,从而提高搜索效率。
(3)使用多个点的搜索信息,具有隐含并行性。传统的优化算法往往是从解空间的一个初始点开始最优解的迭代搜索过程。单个点所提供的搜索信息不多,所以搜索效率不高,还有可能陷入局部最优解而停滞;遗传算法从由很多个体组成的初始种群开始最优解的搜索过程,而不是从单个个体开始搜索。对初始群体进行的、选择、交叉、變異等运算,产生出新一代群体,其中包括了许多群体信息。这些信息可以避免搜索一些不必要的点,从而避免陷入局部最优,逐步逼近全局最优解。
(4) 使用概率搜索而非确定性规则。传统的优化算法往往使用确定性的搜索方法,一个搜索点到另一个搜索点的转移有确定的转移方向和转移关系,这种确定性可能使得搜索达不到最优店,限制了算法的应用范围。遗传算法是一种自适应搜索技术,其选择、交叉、變異等运算都是以一种概率方式进行的,增加了搜索过程的灵活性,而且能以较大概率收敛于最优解,具有较好的全局优化求解能力。但,交叉概率、變異概率等参数也会影响算法的搜索结果和搜索效率,所以如何选择遗传算法的参数在其应用中是一个比较重要的问题。
综上,由于遗传算法的整体搜索策略和优化搜索方式在计算时不依赖于梯度信息或其他辅助知识,只需要求解影响搜索方向的目标函数和相应的适应度函数,所以遗传算法提供了一种求解复杂系統问题的通用框架。它不依赖于问题的具体领域,对问题的种类有很强的鲁棒性,所以广泛应用于各种领域,包括:函数优化、组合优化生产调度问题、自动控制
、機器人學、圖像處理(圖像恢複、圖像邊緣特征提取......)、人工生命、遺傳編程、機器學習。
3 遗传算法的基本流程及实现技术
基本遗传算法(Simple Genetic Algorithms,SGA)只使用选择算子、交叉算子和變異算子这三种遗传算子,进化过程简单,是其他遗传算法的基础。
3.1 遗传算法的基本流程
通過隨機方式産生若幹由確定長度(長度與待求解問題的精度有關)編碼的初始群體;
通過適應度函數對每個個體進行評價,選擇適應度值高的個體參與遺傳操作,適應度低的個體被淘汰;
经遗传操作(复制、交叉、變異)的个体集合形成新一代种群,直到满足停止准则(进化代数GEN>=?);
將後代中變現最好的個體作爲遺傳算法的執行結果。
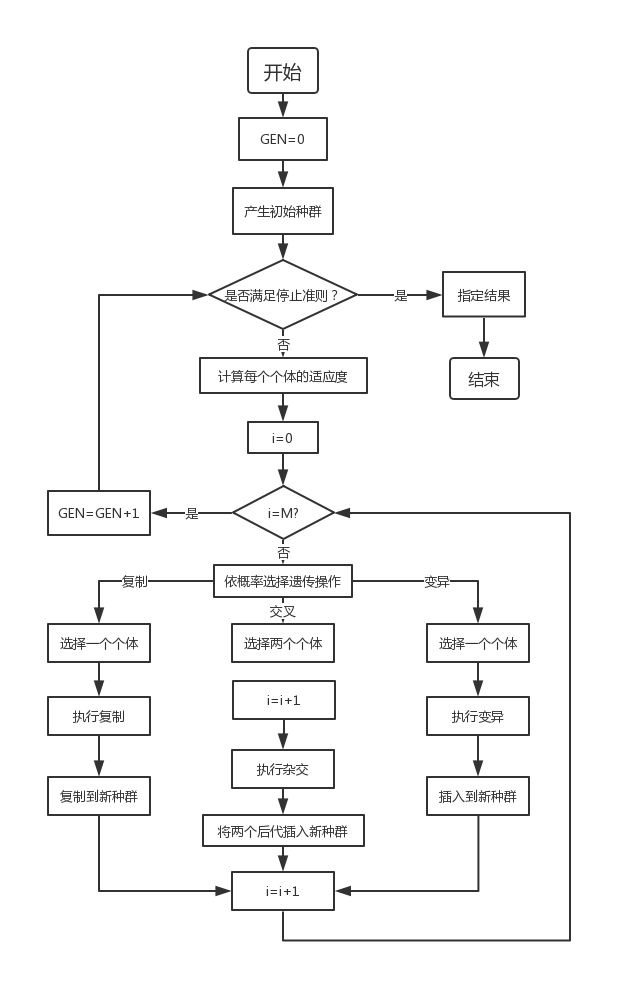
其中,GEN是當前代數;M是種群規模,i代表種群數量。
3.2 遗传算法的实现技术
基本遗传算法(SGA)由编码、适应度函数、遗传算子(选择、交叉、變異)及运行参数组成。
3.2.1 编码
(1)二進制編碼
二進制編碼的字符串長度與問題所求解的精度有關。需要保證所求解空間內的每一個個體都可以被編碼。
優點:編、解碼操作簡單,遺傳、交叉便于實現
缺點:長度大
(2)其他編碼方法
格雷碼、浮點數編碼、符號編碼、多參數編碼等
3.2.2 适应度函数
適應度函數要有效反映每一個染色體與問題的最優解染色體之間的差距。
3.2.3選擇算子

3.2.4 交叉算子
交叉運算是指對兩個相互配對的染色體按某種方式相互交換其部分基因,從而形成兩個新的個體;交叉運算是遺傳算法區別于其他進化算法的重要特征,是産生新個體的主要方法。在交叉之前需要將群體中的個體進行配對,一般采取隨機配對原則。
常用的交叉方式:
單點交叉
雙點交叉(多點交叉,交叉點數越多,個體的結構被破壞的可能性越大,一般不采用多點交叉的方式)
均勻交叉
算術交叉
3.2.5 變異算子
遗传算法中的變異运算是指将个体染色体编码串中的某些基因座上的基因值用该基因座的其他等位基因来替换,从而形成一个新的个体。
就遗传算法运算过程中产生新个体的能力方面来说,交叉运算是产生新个体的主要方法,它决定了遗传算法的全局搜索能力;而變異运算只是产生新个体的辅助方法,但也是必不可少的一个运算步骤,它决定了遗传算法的局部搜索能力。交叉算子与變異算子的共同配合完成了其对搜索空间的全局搜索和局部搜索,从而使遗传算法能以良好的搜索性能完成最优化问题的寻优过程。
3.2.6 运行参数

4 遗传算法的基本原理
4.1 模式定理

4.2 积木块假设
具有低階、定義長度短,且適應度值高于群體平均適應度值的模式稱爲基因塊或積木塊。
积木块假设:个体的基因块通过选择、交叉、變異等遗传算子的作用,能够相互拼接在一起,形成适应度更高的个体编码串。
積木塊假設說明了用遺傳算法求解各類問題的基本思想,即通過積木塊直接相互拼接在一起能夠産生更好的解。
clc;
clear all;
close all;
%----------------参数设置-----------------------
MAXGEN=200; % 最大遗传代数
sizepop=40; % 种群大小
lenchrom=[20 20]; % 每个變量的二进制长度
trace=zeros(1,MAXGEN);
%--------------------------------------------------------------------------
best=struct(‘fitness‘,0,‘X‘,[],‘binary‘,[],‘chrom‘,[]); % 最佳个体 记录其适应度值、十进制值、二进制编码、量子比特编码
%% 初始化种群
chrom=InitPop(sizepop*2,sum(lenchrom));
%% 对种群实施一次测量 得到二进制编码
binary=collapse(chrom);
%% 求种群个体的适应度值,和对应的十进制值
[fitness,X]=FitnessFunction(binary,lenchrom); % 使用目标函数计算适应度
%% 记录最佳个体到best
[best.fitness bestindex]=max(fitness); % 找出最大值
best.binary=binary(bestindex,:);
best.chrom=chrom([2*bestindex-1:2*bestindex],:);
best.X=X(bestindex,:);
trace(1)=best.fitness;
fprintf(‘%d\n‘,1)
%% 进化
for gen=2:MAXGEN
fprintf(‘%d\n‘,gen) %提示进化代数
%% 对种群实施一次测量
binary=collapse(chrom);
%% 计算适应度
[fitness,X]=FitnessFunction(binary,lenchrom);
%% 量子旋轉門
chrom=Qgate(chrom,fitness,best,binary);
[newbestfitness,newbestindex]=max(fitness); % 找到最佳值
% 记录最佳个体到best
if newbestfitness>best.fitness
best.fitness=newbestfitness;
best.binary=binary(newbestindex,:);
best.chrom=chrom([2*newbestindex-1:2*newbestindex],:);
best.X=X(newbestindex,:);
end
trace(gen)=best.fitness;
end
%% 画进化曲线
plot(1:MAXGEN,trace);
title(‘进化过程‘);
xlabel(‘进化代数‘);
ylabel(‘每代的最佳适应度‘);
%% 显示优化结果
disp([‘最优解X:‘,num2str(best.X)])
disp([‘最大值Y:‘,num2str(best.fitness)]);
function chrom=Qgate(chrom,fitness,best,binary)
%% 量子旋轉門调整策略
% 输入 chrom:更新前的量子比特编码
% fitness:适应度值
% best:当前种群中最优个体
% binary:二进制编码
% 输出 chrom:更新后的量子比特编码
sizepop=size(chrom,1)/2;
lenchrom=size(binary,2);
for i=1:sizepop
for j=1:lenchrom
A=chrom(2*i-1,j); % α
B=chrom(2*i,j); % β
x=binary(i,j);
b=best.binary(j);
if ((x==0)&(b==0))||((x==1)&(b==1))
delta=0; % delta为旋转角的大小
s=0; % s为旋转角的符号,即旋转方向
elseif (x==0)&(b==1)&(fitness(i)<best.fitness)
delta=0.01*pi;
if A*B>0
s=1;
elseif A*B<0
s=-1;
elseif A==0
s=0;
elseif B==0
s=sign(randn);
end
elseif (x==0)&(b==1)&(fitness(i)>=best.fitness)
delta=0.01*pi;
if A*B>0
s=-1;
elseif A*B<0
s=1;
elseif A==0
s=sign(randn);
elseif B==0
s=0;
end
elseif (x==1)&(b==0)&(fitness(i)<best.fitness)
delta=0.01*pi;
if A*B>0
s=-1;
elseif A*B<0
s=1;
elseif A==0
s=sign(randn);
elseif B==0
s=0;
end
elseif (x==1)&(b==0)&(fitness(i)>=best.fitness)
delta=0.01*pi;
if A*B>0
s=1;
elseif A*B<0
s=-1;
elseif A==0
s=0;
elseif B==0
s=sign(randn);
end
end
e=s*delta; % e为旋转角
U=[cos(e) -sin(e);sin(e) cos(e)]; % 量子旋轉門
y=U*[A B]‘; % y为更新后的量子位
chrom(2*i-1,j)=y(1);
chrom(2*i,j)=y(2);
end
end
function X=bin2decFun(x,lenchrom,bound)
%% 二进制转化成十进制
% 输入 x:二进制编码
% lenchrom:各變量的二进制位数
% bound:各變量的范围
% 输出 X:十进制数
M=length(lenchrom);
n=1;
X=zeros(1,M);
for i=1:M
for j=lenchrom(i)-1:-1:0
X(i)=X(i)+x(n).*2.^j;
n=n+1;
end
end
X=bound(:,1)‘+X./(2.^lenchrom-1).*(bound(:,2)-bound(:,1))‘;
版本:2014a
【优化算法】量子遗传优化算法【含Matlab源码 1123期】
標簽:方式 變換 變量 不必要 系統 變異 alt 旋轉門 max
原文地址:https://www.cnblogs.com/homeofmatlab/p/14993038.html