標簽:適應 mes 變量 曲線 簡介 原因 好的 不可 over
粒子群优化(PSO)是一种基于群体智能的数值优化算法,由社会心理学家James Kennedy和电气工程师Russell Eberhart于1995年提出。自PSO诞生以来,它在许多方面都得到了改进,这一部分将介绍基本的粒子群优化算法原理和过程。
1.1 粒子群优化
粒子群優化(PSO)是一種群智能算法,其靈感來自于鳥類的群集或魚群學習,用于解決許多科學和工程領域中出現的非線性、非凸性或組合優化問題。

1.1.1 算法思想
許多鳥類都是群居性的,並由各種原因形成不同的鳥群。鳥群可能大小不同,出現在不同的季節,甚至可能由群體中可以很好合作的不同物種組成。更多的眼睛和耳朵意味著有更多的及時發現食物和捕食者的機會。鳥群在許多方面對其成員的生存總是有益的:
覓食:社會生物學家E.O.Wilson說,至少在理論上,群體中的個體成員可以從其他成員在尋找食物過程中的發現和先前的經驗中獲益[1]。如果一群鳥的食物來源是相同的,那麽某些種類的鳥就會以一種非競爭的方式聚集在一起。這樣,更多的鳥類就能利用其他鳥類對食物位置的發現。
抵禦捕食者:鳥群在保護自己免受捕食者侵害方面有很多優勢。
更多的耳朵和眼睛意味著更多的機會發現捕食者或任何其他潛在的危險;
一群鳥可能會通過圍攻或敏捷的飛行來迷惑或壓制捕食者;
在群體中,互相間的警告可以減少任何一只鳥的危險。
空氣動力學:當鳥類成群飛行時,它們經常把自己排成特定的形狀或隊形。鳥群中鳥的數量不同,每只鳥煽動翅膀時産生不同的氣流,這都會導致變化的風型,這些隊形會充分利用不同的分型,從而使得飛行中的鳥類能夠以最節能的方式利用周圍的空氣。
粒子群算法的發展需要模擬鳥群的一些優點,然而,爲了了解群體智能和粒子群優化的一個重要性質,值得提一下是鳥群的一些缺點。當鳥類成群結隊時,也會給它們帶來一些風險。更多的耳朵和眼睛意味著更多的翅膀和嘴,這導致更多的噪音和運動。在這種情況下,更多的捕食者可以定位鳥群,對鳥類造成持續的威脅。一個更大的群體也會需要更多的食物,這導致更多食物競爭,從而可能淘汰群體中一些較弱的鳥類。這裏需要指出的是,PSO並沒有模擬鳥類群體行爲的缺點,因此,在搜索過程中不允許殺死任何個體,而在遺傳算法中,一些較弱的個體會消亡。在PSO中,所有的個體都將存活,並在整個搜索過程中努力讓自己變得更強大。在粒子群算法中,潛在解的改進是合作的結果,而在進化算法中則是因爲競爭。這個概念使得群體智能不同于進化算法。簡而言之,在進化算法中,每一次叠代都有一個新的種群進化,而在群智能算法中,每一代都有個體使自己變得更好。個體的身份不會隨著叠代而改變。Mataric[2]給出了以下鳥群規則:
安全漫遊:鳥類飛行時,不存在相互間或與障礙物間的碰撞;
分散:每只鳥都會與其他鳥保持一個最小的距離;
聚合:每只鳥也會與其他鳥保持一個最大的距離;
歸巢:所有的鳥類都有可能找到食物來源或巢穴。
在設計粒子群算法時,並沒有采用這四種規則來模擬鳥類的群體行爲。在Kennedy和Eberhart開發的基本粒子群優化模型中,對agent的運動不遵循安全漫遊和分散規則。換句話說,在基本粒子群優化算法的運動過程中,允許粒子群優化算法中的代理盡可能地靠近彼此。而聚合和歸巢在粒子群優化模型中是有效的。在粒子群算法中,代理必須在特定的區域內飛行,以便與任何其他代理保持最大距離。這就相當于在整個過程中,搜索始終停留在搜索空間的邊界內或邊界處。第四個規則,歸巢意味著組中的任何代理都可以達到全局最優。
在PSO模型的發展過程中,Kennedy和Eberhart提出了五個判斷一組代理是否是群體的基本原則:
就近原則:代理群體應該能夠進行簡單的空間和時間計算;
質量原則:代理群體能夠對環境中的質量因素作出反應;
多響應原則:代理群體不應在過于狹窄的通道從事活動;
穩定性原則:代理群體不能每次環境變化時就改變其行爲模式;
適應性原则:计算代价不大时,代理群体可以改变其行为模式。
1.1.2 粒子群优化过程
考慮到這五個原則,Kennedy和Eberhart開發了一個用于函數優化的PSO模型。在粒子群算法中,采用隨機搜索的方法,利用群體智能進行求解。換句話說,粒子群算法是一種群智能搜索算法。這個搜索是由一組隨機生成的可能解來完成的。這種可能解的集合稱爲群,每個可能解都稱爲粒子。
在粒子群優化算法中,粒子的搜索受到兩種學習方式的影響。每一個粒子都在向其他粒子學習,同時也在運動過程中學習自己的經驗。向他人學習可以稱爲社會學習,而從自身經驗中學習可以稱爲認知學習。由于社會學習的結果,粒子在它的記憶中存儲了群中所有粒子訪問的最佳解,我們稱之爲gbest。通過認知學習,粒子在它的記憶中儲存了迄今爲止它自己訪問過的最佳解,稱爲pbest。
任何粒子的方向和大小的變化都是由一個叫做速度的因素決定的,速度是位置相對于時間的變化率。對于PSO,叠代的是時間。這樣,對于粒子群算法,速度可以定義爲位置相對于叠代的變化率。由于叠代計數器單位增加,速度v的維數與位置x相同。
对于D维搜索空间,在时间步t下群体中的第ith个粒子由D维向量x i t = ( x i 1 t , ? ? , x i D t ) T x_i^t = {(x_{i1}^t, \cdots ,x_{iD}t)T}xit?=(xi1t?,?,xiDt?)T来表示,其速度由另一个D维向量v i t = ( v i 1 t , ? ? , v i D t ) T v_i^t = {(v_{i1}^t, \cdots ,v_{iD}t)T}vit?=(vi1t?,?,viDt?)T表示。第ith个粒子访问过的最优解位置用p i t = ( p i 1 t , ? ? , p i D t ) T p_i^t = {\left( {p_{i1}^t, \cdots ,p_{iD}^t} \right)^T}pit?=(pi1t?,?,piDt?)T表示,群体中最优粒子的索引为“g”。第ith个粒子的速度和位置分别由下式进行更新:
v i d t + 1 = v i d t + c 1 r 1 ( p i d t ? x i d t ) + c 2 r 2 ( p g d t ? x i d t ) (1) v_{id}^{t + 1} = v_{id}^t + {c_1}{r_1}\left( {p_{id}^t - x_{id}^t} \right) + {c_2}{r_2}\left( {p_{gd}^t - x_{id}^t} \right)\tag 1vidt+1?=vidt?+c1?r1?(pidt??xidt?)+c2?r2?(pgdt??xidt?)(1)
x i d t + 1 = x i d t + v i d t + 1 (2) x_{id}^{t + 1} = x_{id}^t + v_{id}^{t + 1}\tag 2xidt+1?=xidt?+vidt+1?(2)
其中d=1,2,…,D爲維度,i=1,2,…,S爲粒子索引,S是群體大小。c1和c2爲常數,分別稱爲認知和社交縮放參數,或簡單地稱爲加速系數。r1和r2是滿足均勻分布[0,1]之間的隨機數。上面兩個式子均是對每個粒子的每個維度進行單獨更新,問題空間中不同維度之間唯一的聯系是通過目標函數引入的,也就是當前所找到的最好位置gbest和pbest[3]。PSO的算法流程如下:
1.1.3 解读更新等式
速度更新等式(1)的右側包括三部分3:
前一時間的速度v,可以認爲是一動量項,用于存儲之前的運動方向,其目的是防止粒子劇烈地改變方向。
第二項是認知或自我部分,通過這一項,粒子的當前位置會向其自己的最好位置移動,這樣在整個搜索過程中,粒子會記住自己的最佳位置,從而避免自己四處遊蕩。這裏需要注意的是,pidt-xidt是一個方向從xidt到pidt的向量,從而將當前位置向粒子的最佳位置吸引,兩者的順序不能改變,否則當前位置會遠離最佳位置。
第三項是社交部分,負責通過群體共享信息。通過該項,粒子向群體中最優的個體移動,即每個個體向群體中的其他個體學習。同樣兩者應該是pgbt-xidt。
可以看出,認知尺度參數c1調節的是粒子在其最佳位置方向上的最大步長,而社交尺度參數c2調節的是全局最優粒子方向上的最大步長。圖2給出了粒子在二維空間中運動的典型幾何圖形。
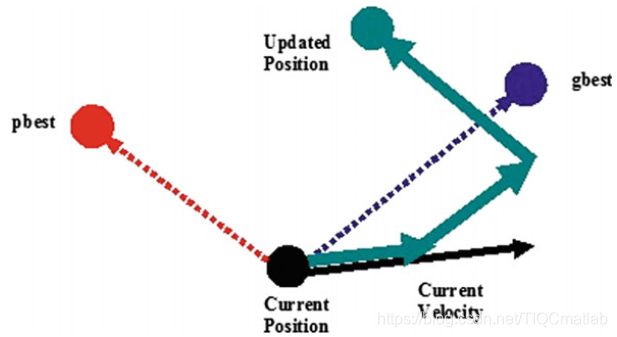
图2 粒子群优化过程中粒子移动的几何说明
从更新方程可以看出,Kennedy和Eberhart的PSO设计遵循了PSO的五个基本原则。在粒子群优化过程中,在d维空间中对一系列时间步进行计算。在任何时间步,种群都遵循gbest和pbest的指导方向,即种群对质量因素作出反应,从而遵循质量原则。由于速度更新方程中有均布随机数r1和r2,在pbest和gbest之间的当前位置随机分配,这证明了响应原理的多样性。在粒子群优化过程中,只有当粒子群从gbest中接收到较好的信息时,才会发生随机运动,从而证明了粒子群优化过程的稳定性原则。种群在gbest变化时发生变化,因此遵循適應性原则。
1.2 粒子群优化中的参数
任何基于種群的算法的收斂速度和尋優能力都受其參數選擇的影響。通常,由于這些算法的參數高度依賴于問題參數,因此不可能對這些算法的參數設置給出一般性的建議。但是,已有的理論和/或實驗研究,給出了參數值的一般範圍。與其他基于種群的搜索算法類似,由于在搜索過程中存在隨機因素r1和r2,因此通用PSO的參數調整一直是一項具有挑戰性的任務。PSO的基礎版本只需要很少的參數。本章只討論了[4]中介紹的PSO基礎版本的參數。
一个基本的参数是群体规模,它通常是根据问题中决策變量的数量和问题的复杂性经验地设置的。一般建议20-50个粒子。
另一个参数是缩放因子c1和c2。如前所述,这些参数决定了下一个迭代中粒子的步长。也就是说,c1和c2决定了粒子的速度。在PSO的基础版本中,选择c1=c2=2。在这种情况下,粒子s速度的增加是不受控制的,这有利于更快的收敛速度,但不利于更好地利用搜索空间。如果我们令c1=c2>0,那么粒子会吸引到pbest和gbest的平均值。c1>c2设置有利于多模态问题,而c2>c1有利于单模态问题。在搜索过程中,c1和c2的值越小,粒子轨迹越平滑,而c1和c2的值越大,粒子运动越剧烈,加速度越大。研究人员也提出了自適應加速系数[5]。
停止准則不僅是粒子群算法的參數,也是任何基于種群的元啓發式算法的參數。常用的停止准則通常基于函數評估或叠代的最大次數,該次數與算法所花費的時間成正比。一個更有效的停止准則是基于算法的搜索能力,如果一個算法在一定的叠代次數內沒有顯著地改進解,那麽應該停止搜索。
clear
clc
fitnessfcn = @ PSO_PID; % 適應度函数句柄
nvars=3; % 个体變量数目
LB = [0 0 0]; % 下限
UB = [300 300 300]; % 上限
options=gaoptimset(‘PopulationSize‘,100,‘PopInitRange‘,[LB;UB],‘EliteCount‘,10,‘CrossoverFraction‘,0.6,‘Generations‘,100,‘StallGenLimit‘,100,‘TolFun‘,1e-100,‘PlotFcns‘,{@gaplotbestf,@gaplotbestindiv}); % 算法参数设置
[x_best,fval]=ga(fitnessfcn,nvars, [],[],[],[],LB,UB,[],options); % 运行遗传算法
%% 清空环境
clear
clc
%% 参数设置
w = 0.6; % 惯性因子
c1 = 2; % 加速常数
c2 = 2; % 加速常数
Dim = 3; % 维数
SwarmSize = 100; % 粒子群规模
ObjFun = @PSO_PID; % 待优化函数句柄
MaxIter = 100; % 最大迭代次数
MinFit = 0.1; % 最小適應值
Vmax = 1;
Vmin = -1;
Ub = [300 300 300];
Lb = [0 0 0];
%% 粒子群初始化
Range = ones(SwarmSize,1)*(Ub-Lb);
Swarm = rand(SwarmSize,Dim).*Range + ones(SwarmSize,1)*Lb % 初始化粒子群
VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) + Vmin % 初始化速度
fSwarm = zeros(SwarmSize,1);
for i=1:SwarmSize
fSwarm(i,:) = feval(ObjFun,Swarm(i,:)); % 粒子群的適應值
end
%% 个体极值和群体极值
[bestf bestindex]=min(fSwarm);
zbest=Swarm(bestindex,:); % 全局最佳
gbest=Swarm; % 个体最佳
fgbest=fSwarm; % 个体最佳適應值
fzbest=bestf; % 全局最佳適應值
%% 迭代寻优
iter = 0;
y_fitness = zeros(1,MaxIter); % 预先产生4个空矩阵
K_p = zeros(1,MaxIter);
K_i = zeros(1,MaxIter);
K_d = zeros(1,MaxIter);
while( (iter < MaxIter) && (fzbest > MinFit) )
for j=1:SwarmSize
% 速度更新
VStep(j,:) = w*VStep(j,:) + c1*rand*(gbest(j,:) - Swarm(j,:)) + c2*rand*(zbest - Swarm(j,:));
if VStep(j,:)>Vmax, VStep(j,:)=Vmax; end
if VStep(j,:)<Vmin, VStep(j,:)=Vmin; end
% 位置更新
Swarm(j,:)=Swarm(j,:)+VStep(j,:);
for k=1:Dim
if Swarm(j,k)>Ub(k), Swarm(j,k)=Ub(k); end
if Swarm(j,k)<Lb(k), Swarm(j,k)=Lb(k); end
end
% 適應值
fSwarm(j,:) = feval(ObjFun,Swarm(j,:));
% 个体最优更新
if fSwarm(j) < fgbest(j)
gbest(j,:) = Swarm(j,:);
fgbest(j) = fSwarm(j);
end
% 群体最优更新
if fSwarm(j) < fzbest
zbest = Swarm(j,:);
fzbest = fSwarm(j);
end
end
iter = iter+1; % 迭代次数更新
y_fitness(1,iter) = fzbest; % 为绘图做准备
K_p(1,iter) = zbest(1);
K_i(1,iter) = zbest(2);
K_d(1,iter) = zbest(3);
end
%% 绘图输出
figure(1) % 绘制性能指标ITAE的变化曲線
plot(y_fitness,‘LineWidth‘,2)
title(‘最优个体適應值‘,‘fontsize‘,18);
xlabel(‘迭代次数‘,‘fontsize‘,18);ylabel(‘適應值‘,‘fontsize‘,18);
set(gca,‘Fontsize‘,18);
figure(2) % 绘制PID控制器参数变化曲線
plot(K_p)
hold on
plot(K_i,‘k‘,‘LineWidth‘,3)
plot(K_d,‘--r‘)
title(‘Kp、Ki、Kd 优化曲線‘,‘fontsize‘,18);
xlabel(‘迭代次数‘,‘fontsize‘,18);ylabel(‘参数值‘,‘fontsize‘,18);
set(gca,‘Fontsize‘,18);
legend(‘Kp‘,‘Ki‘,‘Kd‘,1);
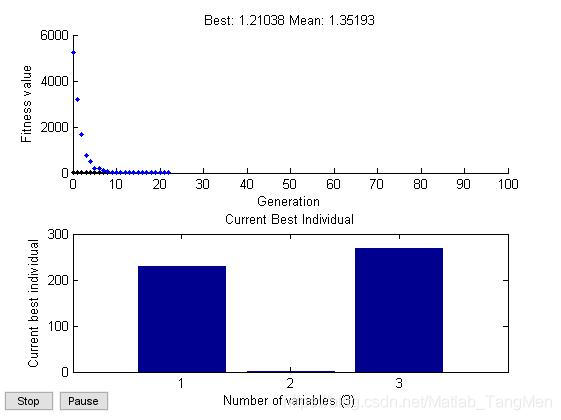
版本:2014a
【PID优化】基于matlab粒子群算法PID控制器优化设计【含Matlab源码 1122期】
標簽:適應 mes 變量 曲線 簡介 原因 好的 不可 over
原文地址:https://www.cnblogs.com/homeofmatlab/p/14993035.html