標簽：type 影響 産生 邏輯 應用 ado text end poster
在本文關于如何在R中進行貝葉斯分析。我們介紹貝葉斯分析，這個例子是關于職業足球比賽的進球數。
首先，我們認爲職業足球比賽的進球數來自分布
，其中θ是平均進球數。現在假設我們用一位足球專家的意見來得出足球比賽的平均進球數，即參數θ，我們得到：
。
curve(dnorm(x, 2.5, 0.2), from = -2, to = 8,...)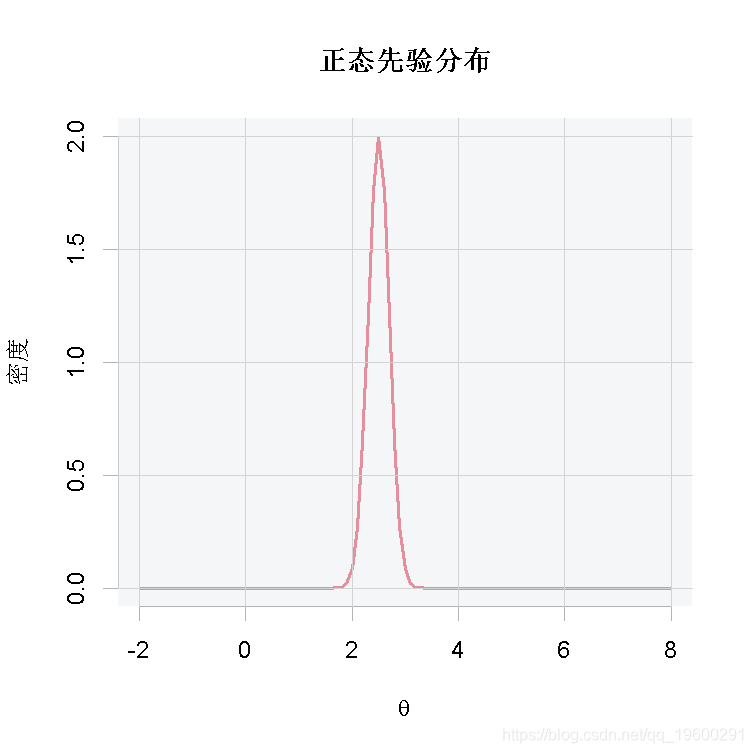 
在這種情況下，我們想知道θ的後驗分布是什麽樣子的，這個分布的平均值是什麽。爲了做到這一點，我們將在三種情況下分析：
我們有1個觀察值x=1，來自分布爲
的總體。
我們有3個觀測值x=c(1,3,5)，來自一個具有分布的總體。
我們有10個觀測值x=c(5,4,3,4,3,2,7,2,4,5)，來自一個具有分布的總體。
在這裏，我想告訴你貝葉斯分析是如何分析的。首先，我們有一個來自具有未知參數θ的泊松分布的人口的似然函數。
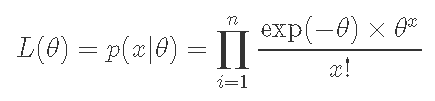
我們知道參數θ的先驗分布p(θ)是由以下公式給出的。
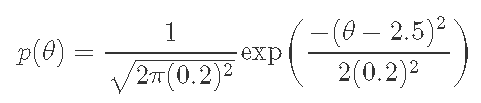
最後，θ的後驗分布爲。
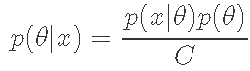
其中常數C的計算方法如下。
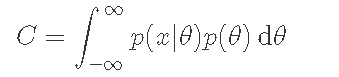
而後驗分布E(θ|x)的平均值由以下公式給出。
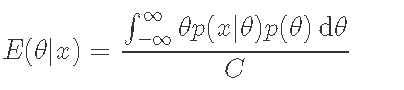
在這裏，你將學習如何在R中使用蒙特卡洛模擬來回答上面提出的問題。對于這三種情況，你將遵循以下步驟。
首先，你需要根據方案定義數據。
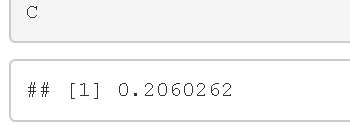
x <- 1 #第一種情況现在使用蒙特卡洛模拟来计算积分。为此，有必要从先验分布中産生N=10000个值θi，并在似然函数
中評估它們。最後，爲了得到C，這些值被平均化。R中的代碼如下。
3. 寻找后验分布
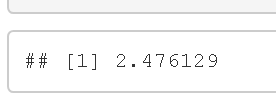
計算完C後，你可以得到後驗分布，如下所示。
最後你可以使用蒙特卡洛模擬計算積分來獲得後驗分布的平均值。
如前所述，上面介紹的代碼用于所有三種情況，唯一根據情況變化的是x。在這一節中，我們將爲每種情況展示一張圖，其中包含θ的先驗和後驗分布、後驗分布的平均值（藍色虛線）和觀測值（粉紅色的點）。
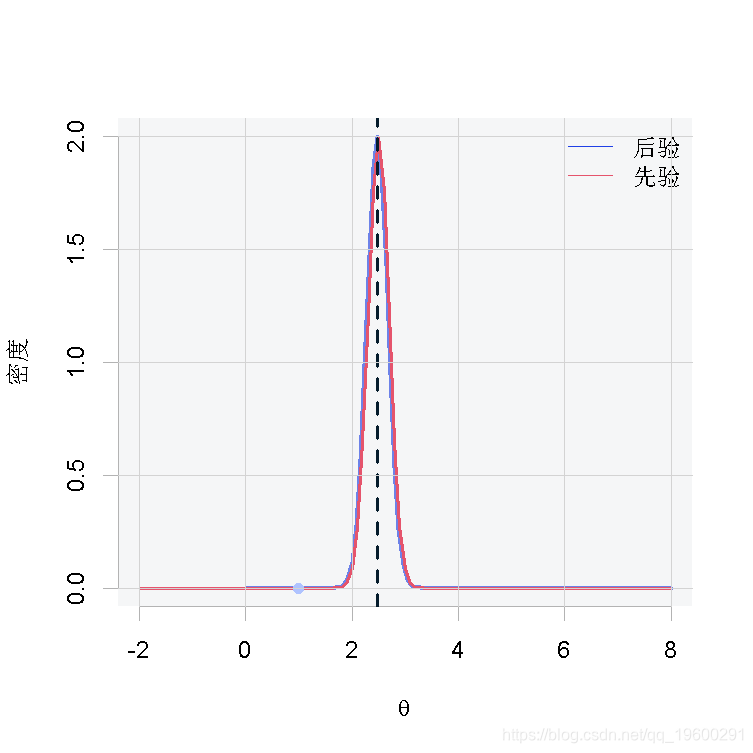
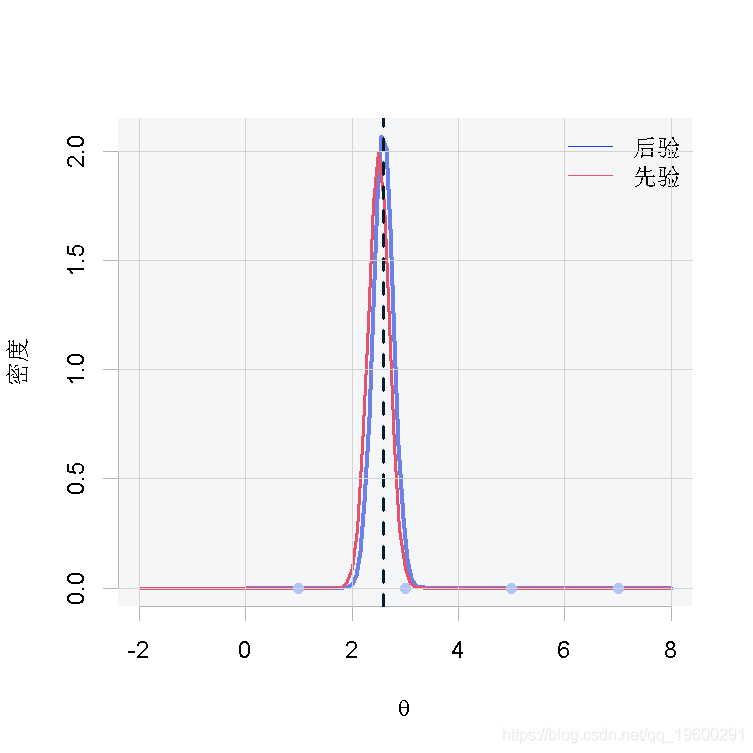
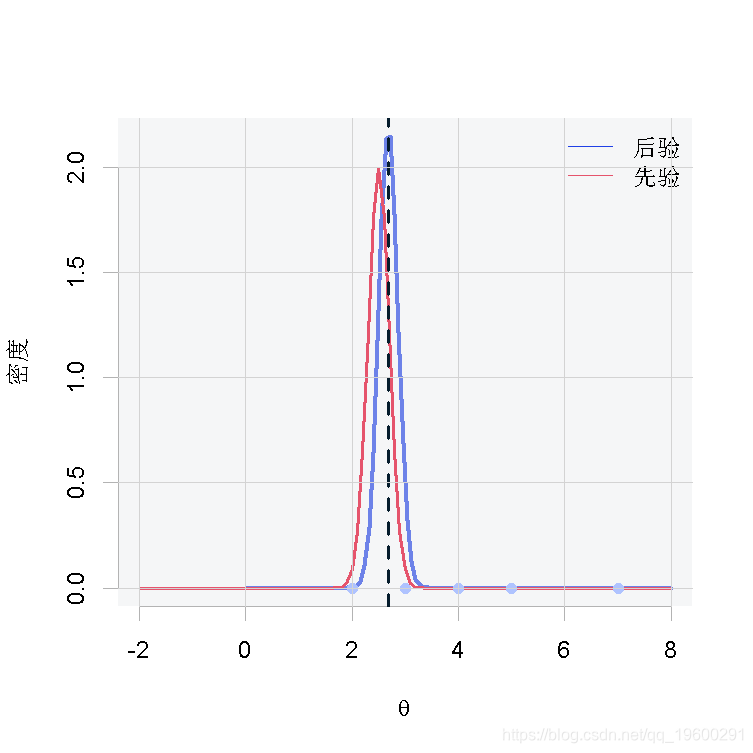
从結果中我们可以得出这样的結論：当我们有很少的观测数据时，如图1和图2，由于缺乏样本证据，后验分布将倾向于类似于先验分布。相反，当我们有大量的观测数据时，如图3，后验分布将偏离先验分布，因为数据将有更大的影響。
我希望你喜歡這篇文章並了解貝葉斯統計。我鼓勵你用其他分布運行這個程序。
最受歡迎的見解
1.R语言多元Logistic邏輯回归 應用案例
2.面板平滑轉移回歸(PSTR)分析案例實現
3.matlab中的偏最小二乘回歸（PLSR）和主成分回歸（PCR）
4.R語言泊松Poisson回歸模型分析案例
5.R語言回歸中的Hosmer-Lemeshow擬合優度檢驗
6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现
7.在R语言中实现Logistic邏輯回归
8.python用線性回歸預測股票價格
9.R語言如何在生存分析與Cox回歸中計算IDI，NRI指標
拓端tecdat|R語言貝葉斯Poisson泊松-正態分布模型分析職業足球比賽進球數
標簽：type 影響 産生 邏輯 應用 ado text end poster
原文地址：https://www.cnblogs.com/tecdat/p/15037034.html
